When you ask cabal-install to install one or more packages, it needs to solve a constraint satisfaction problem: select a version for each of the packages you want to install, plus all their dependencies, such that all version constraints are satisfied. Those version constraints come both from the user (“please install lens version 4”) and from the packages themselves (“this package relies on mtl between version 2.1 and 2.2”). Internally cabal-install uses a modular constraint solver, written by Andres Löh. It was first presented at the Haskell Implementor’s Workshop in 2011, and is based on the paper Modular lazy search for Constraint Satisfaction Problems.
 For the Industrial Haskell Group, Well-Typed has recently extended the constraint solver to deal with qualified goals. In this blog post we will explain how this constraint solver works by means of a running example, and look at how the new qualified goals change things.
For the Industrial Haskell Group, Well-Typed has recently extended the constraint solver to deal with qualified goals. In this blog post we will explain how this constraint solver works by means of a running example, and look at how the new qualified goals change things.
Overview of the Solver
The ability to be able to decouple generating solutions from finding the right one is one of the classical reasons why functional programming matters, and cabal-install’s constraint solver makes very heavy use of this. It first builds a tree with lots of “solutions”; solutions in quotes because many of these solutions will not be valid. It then validates these solutions, marking any invalid ones. This might still leave many possible solutions, so after this we apply some preferences (we prefer newer packages over older ones for example) and heuristics (we want to pick the version of base that is already installed, no point considering others) and then it uses the first solution it finds (if any).
It is very important to realize throughout all this that these trees are never built in their entirety. We depend on laziness to only evaluate as much as necessary. A key design principle throughout the solver is that we must have enough information at each node in the tree to be able to make local decisions. Any step that would require looking at the tree in its entirety would be a big no-no.
In the remainder of this section we will see what these different steps look like using a running example.
Building the tree
Suppose we have a package database with base version 4.0, mtl versions 1.0 and 2.0, both of which depend on base, and a package foo that depends on both base and mtl version 2.0.
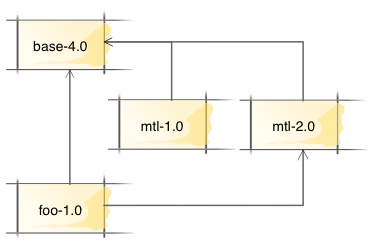
When we ask cabal to install package foo, it constructs a search tree that looks something like this:
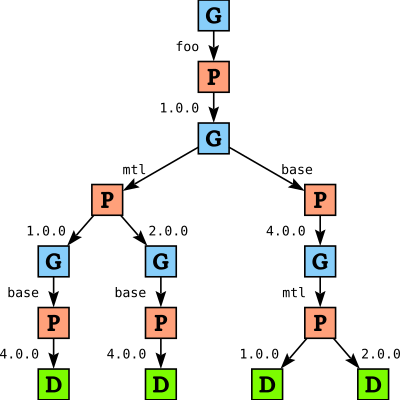
GoalChoice nodes, shown as G nodes in the diagram, represent points where we decide on which package to solve for next. Initially we have only one option: we need to solve for package foo. Similarly, PChoice nodes P represent points where we decide on a package version. Since there is only one version of foo available, we again only have one choice.
Once we have chosen foo version 1.0, we need to solve for foo's dependencies: base and mtl. We don’t know which we should solve for first; the order in which we consider packages may affect how quickly we find a solution, and which solution we return (since we will eventually report the first solution we find). When we build the tree we essentially make a arbitary decision (depending on which order we happen to find the dependencies), and we record the decision using a GoalChoice node. Later we can traverse the tree and apply local heuristics to these GoalChoice nodes (for instance, we might want to consider base before mtl).
In the remainder of the tree we then pick a version for mtl (here we do have a choice in version), and then a version for base, or the other way around. Note that when we build the tree, package constraints are not yet applied: in the tree so far there is nothing that reflects the fact that foo wants version 2.0 of mtl, and every path ends with a Done node D, indicating success. Indeed, we would get precisely the same tree if we have a package DB
where foo depends on either version of mtl.
Validation
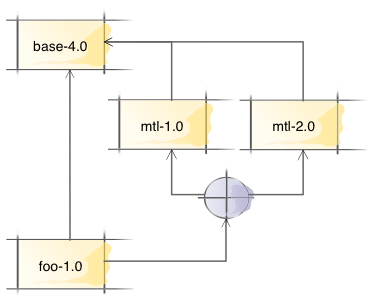
Once we have built the tree, we then walk over the tree and verify package constraints. As soon as we detect a violation of a constraint on a given path we replace that node in the tree with a failure node. For the above example this gives us the following tree:
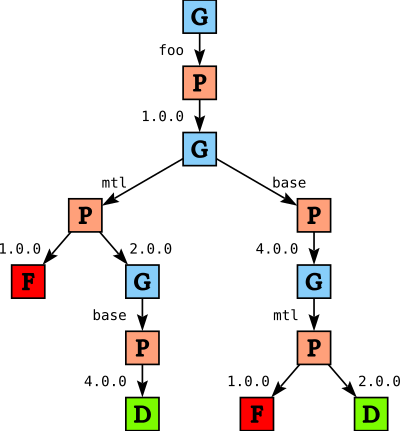
Paths through the tree that lead to failure are not removed from the tree, but are replaced by explicit failure F. This helps with generating a good error message if we fail to find a solution. In this case, both failures are essentially the same problem: we cannot pick version 1.0 for mtl because foo needs version 2.0.
Heuristics and Preferences
After validation we apply a number of heuristics to the tree. For example, we prefer to pick a version of base early because there is generally only one version of base available in the system. In addition, we apply user preferences; for example, we try newer versions of packages before older versions. For our example this gives us
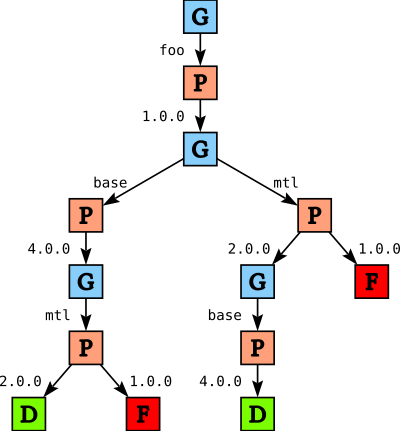
Finding a solution
After applying the heuristics we throw away all but the first choice in each GoalChoice node (but keeping all choices in the PChoice nodes)
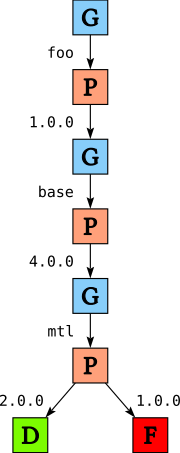
and traverse the tree depth first to find a solution, returning the first solution we find. In our running example, this means that we will use version 1.0 of foo, 4.0 of base and 2.0 of mtl.
Whenever we encounter a Fail node we backtrack. This backtracking is aided by so-called conflict sets. I haven’t shown these conflict sets in the diagrams, but each Fail node in the tree is annotated with a conflict set which records why this path ended in failure. In our running example the conflict set for both Fail nodes is the set {foo, mtl}, recording that there is a conflict between the versions of mtl and the version of foo that we picked. The conflict set is used to guide the backtracking; any choice that we encounter while backtracking that does not involve any variables in the conflict set does not need to be reconsidered, as it would lead to the same failure.
If we cannot find any solution, then we must report an error. Reporting a good error here however is difficult: after all, we have a potentially very large tree, with lots of different kinds of failures. Constructing an informative error from this is difficult, and this is one area where cabal-install might still be improved.
Qualified goals
Motivation
Normally cabal-install can only pick a single version for each package. For example, if we have a situation
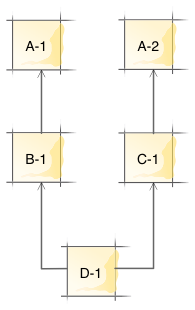
we cannot install package D because it would require installing both versions 1.0 and 2.0 of package A (this is known as the diamond problem).
Setup scripts
Cabal packages can however have their own custom Setup scripts, when necessary, which are Cabal’s equivalent of the traditional ./configure scripts. In principle there should be no problem building these Setup scripts using different (and possibly conflicting) dependencies than the library itself; after all, the Setup script is completely independent from the library.
From Cabal 1.23 and up these setup scripts can have their own list of dependencies. Let’s suppose that in our running example the Setup script of foo has a dependency on any version of mtl:
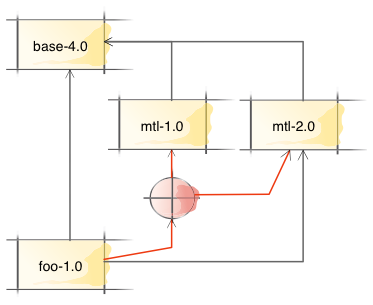
We want to allow the setup script to be compiled against a different version of mtl as foo itself, but of course we would prefer not to, in order to avoid unnecessary additional compilation time.
Qualification
In order to allow picking a different version, we introduce qualified goals for each of the setup dependencies. In our running example, this means that cabal-install will now try to solve for the variables foo, mtl, and base, as well as foo.setup.mtl and foo.setup.base. This makes it possible to pick one version for mtl and another for foo.setup.mtl.
Linking
But how do we make sure that we pick the same version when possible? One (non-) option is to look at the entire search tree and find the solution that installs the smallest number of packages. While that might work in theory, it violates the earlier design principle we started with: we only ever want to make local decisions. The search tree can be quite large; indeed, the addition of the single setup dependency to foo already makes the tree much larger, as we shall see shortly. We certainly never want to inspect the entire search tree (or, worse yet, have the entire search tree in memory).
Instead, we introduce the concept of linking. This means that when we select a version for foo.setup.mtl (say), in addition to being able to pick either version 1.0 or 2.0, we can also say “link the version of foo.setup.mtl to the version of mtl” (provided that we already picked a version for mtl).
Then we can make local decisions: when we pick a version, we prefer to link whenever possible. Of course, this is subject to certain constraints. In the remainder of this section we shall see how qualified goals and linking works using our running example, and identify some of these linking constraints.
Building the tree
The code to build the initial tree is modified to introduce qualified constraints for setup dependencies, but does not itself deal with linking. Instead, it builds the tree as normal, and we then add additional linking options into the tree as a separate phase.
The search tree for our running example gets much bigger now due to combinational explosion: we have two additional variables to solve for, and linking means we have more choices for package versions. Here’s part of the initial search tree:
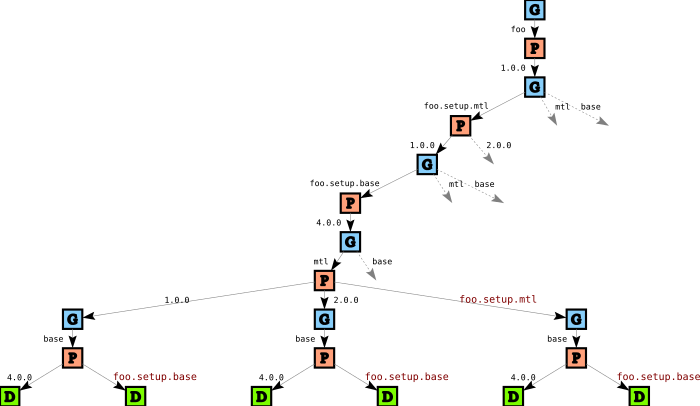
Let’s follow along the spine of this tree to see what’s going on. We first consider foo and pick version 1.0, just like before (there is no other choice). Then, on this path, we first consider foo.setup.mtl, and we have two options: we can either pick version 1.0 or version 2.0. We pick version 1.0, and continue with foo.setup.base and pick version 4.0 (only one option).
But when we now consider mtl things are more interesting: in addition to picking versions 1.0 and 2.0, we can also decide to link the version of mtl against the version of foo.setup.mtl (indicated by a red label in the tree). Similarly, when we pick a version for base, we can now choose to link base against the version of foo.setup.base in addition to picking version 4.0.
Validation
When we link mtl against foo.setup.mtl, we are really saying “please use the exact same package instance for both mtl and foo.setup.mtl”. This means that the dependencies of mtl must also be linked against the dependencies of foo.setup.mtl.
In addition, ghc enforces a so-called single instance restriction. This means that (in a single package database) we can only have one instance of a particular package version. So, for example, we can have both mtl version 1.0 and mtl version 2.0 installed in the same package database, but we cannot have two instance of mtl version 2.0 (for instance, one linked against version 3.0 of transformers and one linked against version 4.0 oftransformers) installed at the same time. Lifting this restriction is an important step towards solving Cabal Hell, but for now we have to enforce it. In our terminology, this means that when we have to solve for both (say) mtl and foo.setup.mtl, we can either pick two different versions, or we can link one to the other, but we cannot pick the same version for both goals.
So, in addition to the regular validation phase which verifies package constraints, we introduce a second validation phase that verifies these kinds of “linking constraints”. We end up with a tree such as
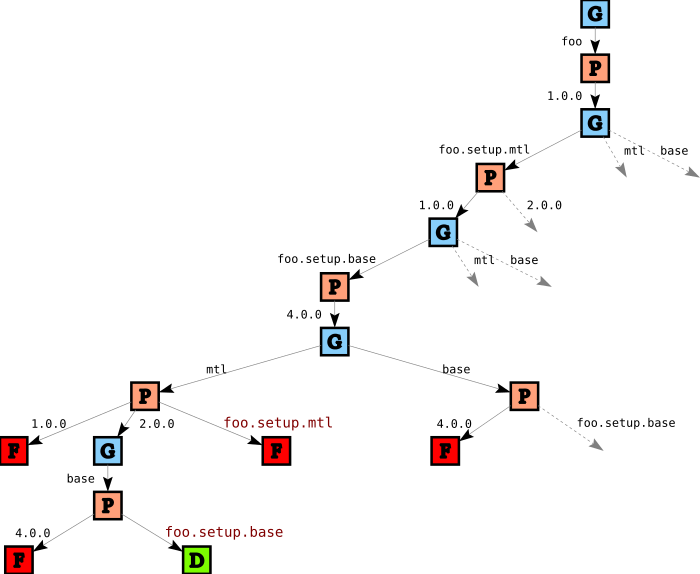
In this part of the tree, the two failures for mtl are because we picked version 1.0 for foo.setup.mtl, but since foo itself wants mtl version 2.0, we cannot pick version 1.0 for goal mtl nor can we link mtl to foo.setup.mtl. The two failures for base are due to the single instance restriction: since we picked version 4.0 for foo.setup.base, we must link base to foo.setup.base.
Heuristics
If we picked the first solution we found in the tree above, we would select version 1.0 of mtl for foo’s setup script and version 2.0 of mtl for foo itself. While that is not wrong per se, it means we do more work than necessary. So, we add an additional heuristic that says that we should consider setup dependencies after regular (library) dependencies. After we apply this heuristic (as well as all the other heuristics) we end up with
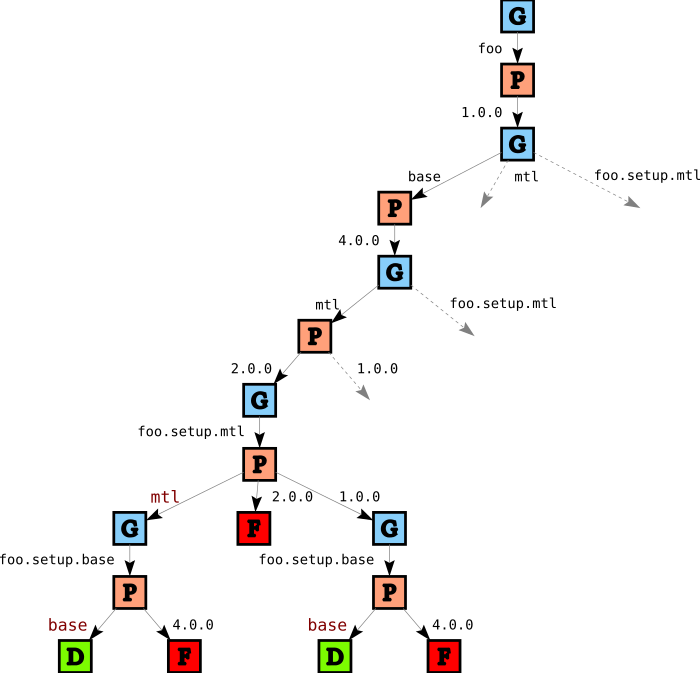
In this part of the tree we see one failure for foo.setup.mtl and two failures for foo.setup.base. The failure for foo.setup.mtl comes from the single instance restriction again: since we picked version 2.0 for mtl, we cannot pick an independent instance for foo.setup.mtl. The failure for foo.setup.base on the right is due to the same reason, but there is an additional reason for the left failure: since we chose to link foo.setup.mtl to mtl, its dependencies (in this case, foo.setup.base) must also be linked.
Finding a solution
As before, after applying the heuristics we prune
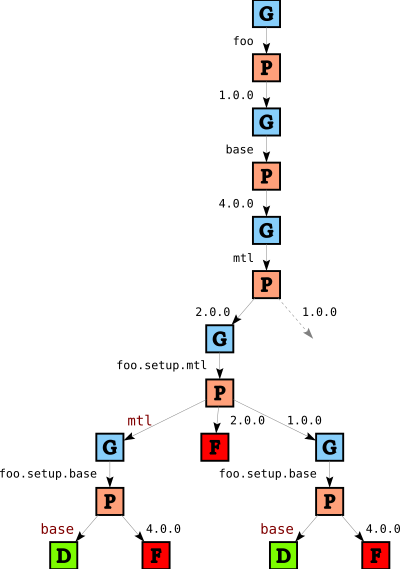
and we report the first solution we find. In this case, this means that we will pick version 2.0 for mtl and link foo.setup.mtl to mtl, and foo.setup.base to base.
Conclusions
Although we skimmed over many details, we covered the most important design principles behind the solver and the new implementation of qualified goals. One thing we did not talk about in this blog post are flag assignments; when the solver needs to decide on the value for a flag, it introduces a FChoice node into the tree with two subtrees for true and false, and then proceeds as normal. When we link package P to package Q, we must then also verify that their flag assignments match.
Qualified goals and linking are now used for setup dependencies, but could also be used to deal with private dependencies, to split library dependencies from executable dependencies, to deal with the base-3 shim package, and possibly other purposes. The modular design of the solver means that such features can be added (mostly) as independent units of code. That doesn’t of course necessarily mean the code is also easy; making sure that all decisions remain local can be a subtle problem. Hopefully this blog post will make the solver code easier to understand and to contribute to.
