Master-Slave, Work-Stealing and Work-Pushing
In this series (2,3,4) of blog posts we will describe a number of basic communication patterns in Cloud Haskell. We don't assume much familiarity with Cloud Haskell, but it will probably be useful to be familiar with the basics; Towards Haskell in the Cloud (Epstein, Black and Peyton Jones, Haskell Symposium 2011) is a good starting point. We will start simple but we will finish with some more advanced techniques.
Source The source code for these examples is available:
cabal unpack http://well-typed.com/blog/aux/files/cloud-demos.tar.gz(The code is also available on github)
Disclaimer The examples in this blog post and in the
distributed-process-demospackage are written for educational purposes; they are not engineered for optimal performance.
Master-Slave
Master-Slave is one of the simplest communication patterns possible. A single master process spawns a bunch of slave processes to do computations on other nodes, and then combines the results.
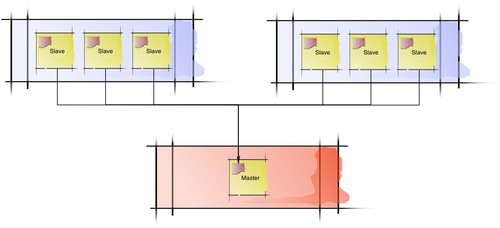
A single master node (red) and a bunch of slave nodes (blue). A single master process spawns a bunch of slave processes, one for each subcomputation. The slave processes post the partial results on the message queue of the master node.
For example, consider summing the number of prime factors of the natural numbers 1 to 100 (why you would want do to that is anyone's guess :) We're just keeping CPUs busy). A master process can spawn a child process on remote nodes for each of the numbers in the sequence, then collect the results and return their sum. The implementation of the slave is very simple:
slave :: (ProcessId, Integer) -> Process () slave (pid, n) = send pid (numPrimeFactors n)
remotable ['slave]
Recall from Towards Haskell in the Cloud that in order to spawn a process on
a node we need something of type Closure (Process ()). In
distributed-process if f : T1 -> T2 then
$(mkClosure 'f) :: T1 -> Closure T2
That is, the first argument the function we pass to mkClosure will act as the
closure environment for that process; if you want multiple values in the
closure environment, you must tuple them up. In this case, the closure
environment will contain the process ID of the master and a natural number that
the slave process must factorize.
The master process is a bit longer but not much more complicated:
master :: Integer -> [NodeId] -> Process Integer master n slaves = do us <- getSelfPid
-- Spawn slave processes to compute numPrimeFactors 1 .. numPrimeFactors n
spawnLocal $
forM_ (zip [1 .. n] (cycle slaves)) $ \(m, them) ->
spawn them ($(mkClosure 'slave) (us, m))
-- Wait for the result sumIntegers (fromIntegral n)
sumIntegers :: Int -> Process Integer
sumIntegers = go 0
where
go :: Integer -> Int -> Process Integer
go !acc 0 = return acc
go !acc n = do
m <- expect
go (acc + m) (n - 1)
We have n bits of work to distribute amongst the slaves, which we do by
zipping [1 .. n] and cycle slaves to get something like
[(1, slave1), (2, slave2), (3, slave3), (4, slave1), (5, slave2), ...
For each of these bits of work we spawn a separate process on the slave node, all of which will run concurrently. This may be too resource intensive (for instance, if each computation would be memory hungry). We will consider a solution to that problem in the next section.
The partial results arrive back at the master node in arbitrary order; this
does not matter because the result of addition does not depend on the order of
the arguments. We spawn the slaves in a separate process (using spawnLocal)
so that the master process can start collecting partial results while it is
still spawning more slaves.
Work-Pushing
If we spawn a separate process for each computation then all these computations run concurrently, which may be too resource intensive. We can instead spawn a single child process on each of the slave nodes, and ask each of those slave processes to factorize a bunch of numbers:
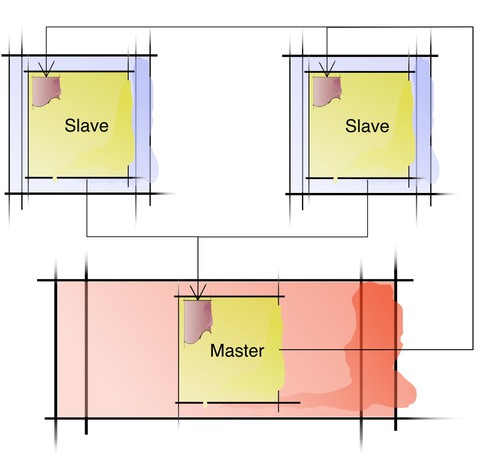
As before, we have a number of slave nodes (blue) and a single master node (red), but now we only have a single slave process on each slave node. The master process pushes the computations to be done to the message queues of the slave processes, which will process them one by one and push the partial results back on the message queue of the master process.
The slave processes wait repeatedly for an integer n and compute
numPrimeFactors n. The closure environment for the slave (the first
argument) now only contains the process ID of the master, because the slave
receives the natural number to factorize by message:
slave :: ProcessId -> Process () slave them = forever $ do n <- expect send them (numPrimeFactors n)
remotable ['slave]
The master process starts one of these slave processes on each of the slave
nodes, distributes the integers [1 .. 100] among them and waits for the
results.
master :: Integer -> [NodeId] -> Process Integer master n slaves = do us <- getSelfPid
-- Start slave processes slaveProcesses <- forM slaves $ \nid -> spawn nid ($(mkClosure 'slave) us)
-- Distribute 1 .. n amongst the slave processes forM_ (zip [1 .. n] (cycle slaveProcesses)) $ \(m, them) -> send them m
-- Wait for the result sumIntegers (fromIntegral n)
Exercise 1: The slave processes keep running even when the master process finishes. How would you modify this example so that they are terminated when they are no longer necessary?
The master pushes all bits of work to be done to the slaves up front. These messages will sit in the slaves' message queues until they are processed. If the messages are big then it might be more efficient to incrementally send messages to slaves.
Exercise 2: (More difficult) Modify the master so that the slaves will only have a limited number of messages waiting in their queue (this means that the master will need to know the sender slave of each reply). (An alternative solution is to switch from work-pushing to work-stealing, which we discuss in the next section).
Note on reliability In the Master-Slave example, if one slave process dies we can restart it to redo that single computation. Restarting is more tricky in the Work-Pushing setup, because a single process is responsible for a large amount of work.
Work-Stealing
A disadvantage of both the master-slave setup and the work-pushing setup is that the master node must decide, a priori, what each slave is going to do. Unless the master node can predict accurately how long each computation will take, it is likely that this leaves some slaves twidling their thumbs while others are buried in work.
One way to avoid this problem is to have the slaves ask the master for work whenever they're ready. This is a simple but effective way of achieving load balancing.
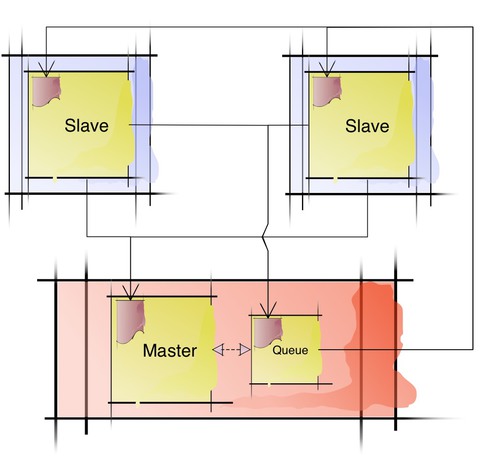
A single master node (red) and a bunch of slave nodes (blue). Each of the slave nodes runs a single slave process. The master node does not push work to the slaves, but rather the slaves query the master for work. To simplify the design, the master process spawns an auxiliary "work queue" process that the slave processes query for the next bit of work to do. This auxiliary process replies to the slave process which then does the work, posts the partial result to the master process message queue, and queries the "work queue" process for more work.
slave :: (ProcessId, ProcessId) -> Process ()
slave (master, workQueue) = do
us <- getSelfPid
go us
where
go us = do
-- Ask the queue for work
send workQueue us
-- If there is work, do it, otherwise terminate
receiveWait
[ match $ \n -> send master (numPrimeFactors n) >> go us
, match $ \() -> return ()
]
remotable ['slave]
The slave is passed the process ID of the process that it can query for more
work, as well as the process ID of the master. When it receives an integer it
factorizes it, sends the number of prime factors to the master process, and
then asks the work queue process for the next bit of work; when it receives a
unit value () it terminates.
master :: Integer -> [NodeId] -> Process Integer master n slaves = do us <- getSelfPid
workQueue <- spawnLocal $ do
-- Return the next bit of work to be done
forM_ [1 .. n] $ \m -> do
them <- expect
send them m
-- Once all the work is done tell the slaves to terminate
forever $ do
pid <- expect
send pid ()
-- Start slave processes forM_ slaves $ \nid -> spawn nid ($(mkClosure 'slave) (us, workQueue))
-- Wait for the result sumIntegers (fromIntegral n)
The master process needs to do two things concurrently: it needs to make sure that slave nodes can ask for more work to do, and it needs to collect the partial results from the slaves. We could do this in a single process, but the design above is much simpler: the master spawns an auxiliary process whose sole purpose is to provide the slaves with more work when they request it; the master process itself meanwhile waits for the partial results from the slaves, as before.
The master spawns a local process which the slaves can query for work; it just
sends out the integers [0 .. 100] in order to whomever asks nexts. It then
starts the slaves, waits for results, and returns the sum.
Exercise 3: Does the above implementation of the master process guarantee that all slave nodes will be properly terminated?
Exercise 4: A downside of this approach compared to the work-pushing approach above is that the latency between computations by each slave is higher: when one computation completes, the slaves must wait for a reply from the work queue process before the next can start. How might you improve this?
To be continued
In the next blog post we will analyze the performance and memory usage of these communication patterns in more detail.
