Announcing the optics library

We are delighted to announce the first Hackage release of optics, a Haskell library for defining and using lenses, traversals, prisms and other optic kinds. The optics library is broadly similar in functionality to the well-established lens library, but uses an abstract interface rather than exposing the underlying implementation of each optic kind. It aims to be easier to understand than lens, with clearer interfaces, simpler types and better error messages, while retaining as much functionality as possible. It is being developed by Andrzej Rybczak and Adam Gundry, with significant contributions from Oleg Grenrus and Andres Löh, and much copy-pasting of code and selective copying of ideas from lens.

Example of optics types and error messages

Let’s dive straight into an example of using optics in GHCi. What is a lens?

*Optics> :info Lens
type Lens s t a b = Optic A_Lens NoIx s t a b

The Optic newtype unifies different optic kinds such as lenses, traversals and prisms. Its first type parameter, here A_Lens, indicates the optic kind in use. The second, NoIx, means that this is not an indexed optic (we will mostly ignore indexed optics for the purposes of this post). As in lens, the s and t parameters represent the types of the outer structure (before and after a type-changing update), and the a and b parameters represent the types of the inner field.

A lens can be constructed using, naturally enough, the lens function, which takes getter and setter functions and returns a Lens (i.e. an Optic A_Lens):

*Optics> :type lens
lens :: (s -> a) -> (s -> b -> t) -> Lens s t a b
*Optics> let l = lens (\(x,_) -> x) (\(_,y) x -> (x,y))
l :: Lens (a1, b) (a2, b) a1 a2

Given a lens we can use it to view the inner value within the outer structure, or set a new value:

*Optics> :type view
view :: Is k A_Getter => Optic' k is s a -> s -> a
*Optics> :type set
set :: Is k A_Setter => Optic k is s t a b -> b -> s -> t

Notice that these types are polymorphic in the optic kind k they accept, but specify very clearly what kind of optic they require.¹ You can apply view to any optic kind k that can be converted to (i.e. is a subtype of) a Getter. The Is constraint implements subtyping using the typeclass system. In particular, we have instances for Is A_Lens A_Getter and Is A_Lens A_Setter so our lens l can be used with both operators:

*Optics> view l ('a','b')
'a'
*Optics> set l 'c' ('a','b')
('c','b')

If you try to use an optic kind that is not a subtype of the required type, a clear error message is given:

*Optics> :type sets
sets :: ((a -> b) -> s -> t) -> Setter s t a b
*Optics> :type view (sets fmap)

<interactive>:1:1: error:
    • A_Setter cannot be used as A_Getter
    • In the expression: view (sets fmap)

Composing optics

Optics are not functions, so they cannot be composed with the (.) operator. This may be viewed as a price to pay for the improved type inference and clearer type errors, but it is conceptually important: we regard optics as an abstract concept distinct from possible representations using functions, so it does not make sense to compose them with function composition or apply them with function application.²

Instead of (.), a separate composition operator (%) is provided:³

*Optics> :type l % l
l % l :: Optic A_Lens '[] ((a, b1), b2) ((b3, b1), b2) a b3
*Optics> view (l % l) (('x','y'),'z')
'x'

Composing optics of different kinds is fine, provided they have a common supertype, which the composition returns:

*Optics> :type l % sets fmap
l % sets fmap
  :: Functor f => Optic A_Setter '[] (f a, b1) (f b2, b1) a b2

However, some optic kinds do not have a common supertype, in which case a type error results from trying to compose them:

*Optics> :type to
to :: (s -> a) -> Getter s a
*Optics> :type to fst % sets fmap

<interactive>:1:1: error:
    • A_Getter cannot be composed with A_Setter
    • In the expression: to fst % sets fmap

The type of (%) itself is not entirely trivial. It relies on a type family Join to calculate the least upper bound of a pair of optic kinds:

*Optics> :type (%)
(%)
  :: (Is k (Join k l), Is l (Join k l)) =>
     Optic k is s t u v
     -> Optic l js u v a b -> Optic (Join k l) (Append is js) s t a b

However, you rarely work with (%) directly, and see only the results. The Join type family can be evaluated directly to determine how two optic kinds compose:

*Optics> :kind! Join A_Lens A_Setter
Join A_Lens A_Setter :: *
= A_Setter
*Optics> :kind! Join A_Getter A_Setter
Join A_Getter A_Setter :: *
= (TypeError ...)

A little lens comparison

For comparison, let’s try the same sequence of commands with lens. Here the underlying implementation using the van Laarhoven representation is rapidly visible:

Control.Lens> :info Lens
type Lens s t a b =
  forall (f :: * -> *). Functor f => (a -> f b) -> s -> f t
Control.Lens> :type lens
lens
  :: Functor f => (s -> a) -> (s -> b -> t) -> (a -> f b) -> s -> f t
Control.Lens> let l = lens (\(x,_) -> x) (\(_,y) x -> (x,y))
l :: Functor f => (a1 -> f a2) -> (a1, b) -> f (a2, b)

Using view and set is not much different:⁴

Control.Lens> :type view
view
  :: Control.Monad.Reader.Class.MonadReader s m =>
     Getting a s a -> m a
Control.Lens> :type set
set :: ASetter s t a b -> b -> s -> t
Control.Lens> view l ('a','b')
'a'
Control.Lens> set l 'c' ('a','b')
('c','b')

However, attempting to use a Setter where a Getter is expected does not report an error immediately, and when it does, the message is somewhat inscrutable:

Control.Lens> :type sets
sets
  :: (Profunctor p, Profunctor q, Settable f) =>
     (p a b -> q s t) -> Optical p q f s t a b
Control.Lens> :type view (sets fmap)
view (sets fmap)
  :: (Control.Monad.Reader.Class.MonadReader (f b) m,
      Settable (Const b), Functor f) =>
     m b
Control.Lens> view (sets fmap) ('x','y')

<interactive>:82:7: error:
    • No instance for (Settable (Const Char))
        arising from a use of ‘sets’
...

Somewhat magically, lens uses the (.) function composition operator for optic composition:

Control.Lens> :type l . l
l . l
  :: Functor f => (a1 -> f a2) -> ((a1, b1), b2) -> f ((a2, b1), b2)
Control.Lens> view (l . l) (('x','y'),'z')
'x'

Even more magically, this automatically selects the appropriate supertype when composing different optic kinds:

Control.Lens> :type l . sets fmap
l . sets fmap
  :: (Settable f1, Functor f2) =>
     (a -> f1 b1) -> (f2 a, b2) -> f1 (f2 b1, b2)

Once more, however, illegitimate compositions are not detected immediately but lead to a type with class constraints that can never be usefully satisfied:

Control.Lens> :type to
to :: (Profunctor p, Contravariant f) => (s -> a) -> Optic' p f s a
Control.Lens> :type to fst . sets fmap
to fst . sets fmap
  :: (Contravariant f1, Settable f1, Functor f2) =>
     (b1 -> f1 b1) -> (f2 b1, b2) -> f1 (f2 b1, b2)

Overloaded labels

Suppose we define two datatypes with the same field name:

data Human = Human { name :: String } deriving Show
data Pet = Pet { name :: String } deriving Show

Now we have a problem if we try to use name as a record selector or in a record update, because it is ambiguous which datatype is meant. The DuplicateRecordFields GHC extension can help with this to some extent, but it makes very limited use of type information to resolve the ambiguity. For example, name (Human "Peter" :: Human) will work but name (Human "Peter") is still considered ambiguous.

The GHC OverloadedLabels extension is intended to help in this situation, by providing a new syntax #name for an “overloaded label” whose interpretation is determined by its type. In particular, we can use overloaded labels as optics by giving instances of the LabelOptic class, with a few GHC extensions and a bit of boilerplate:⁵

{-# LANGUAGE OverloadedLabels DataKinds FlexibleInstances MultiParamTypeClasses
             UndecidableInstances TypeFamilies #-}
instance (a ~ String, b ~ String) => LabelOptic "name" A_Lens Human Human a b where
  labelOptic = lens (\ (Human n) -> n) (\ _h n -> Human n )
instance (a ~ String, b ~ String) => LabelOptic "name" A_Lens Pet Pet a b where
  labelOptic = lens (\ (Pet n) -> n) ( \ _p n -> Pet n )

Now we can use #name as a Lens, and the types will determine which field of which record is intended:

*Optics> view #name (Human "Peter")
"Peter"
*Optics> set #name "Goldie" (Pet "Sparky")
Pet {name = "Goldie"}

For more details on the support for overloaded labels in optics, check out the Haddocks for Optics.Label.

The hierarchy of optics

In optics, the hierarchy of optic kinds is closed, i.e. it is not possible to discover and make use of new optic kinds without modifying the library. Our aim is to make it easier to understand the interfaces and uses of different optic kinds, but this comes at the cost of obscuring some of the underlying common structure of the van Laarhoven or profunctor representations. One concrete limitation relative to lens is that we have not yet explored support for non-empty folds and traversals (Fold1 and Traversal1).

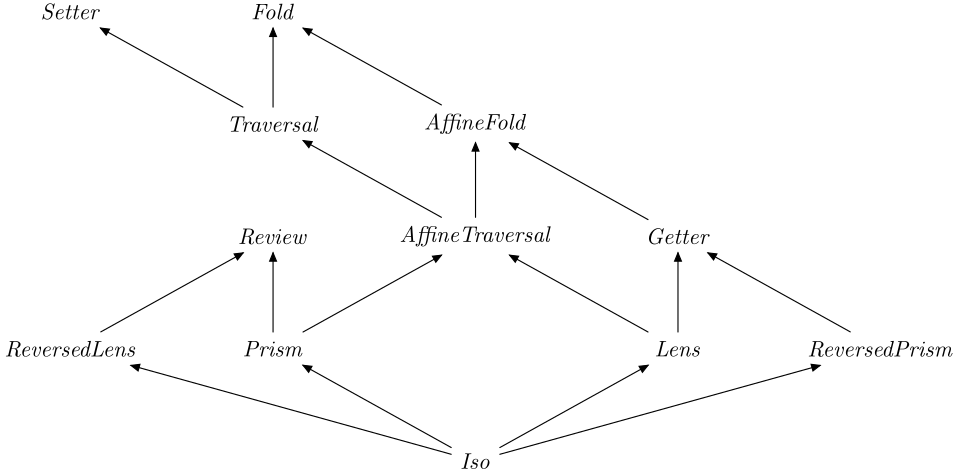
The diagram below shows the hierarchy of optic kinds supported by the initial release. Each arrow points from a subtype to its immediate supertype, e.g. every Lens can be used as a Getter:

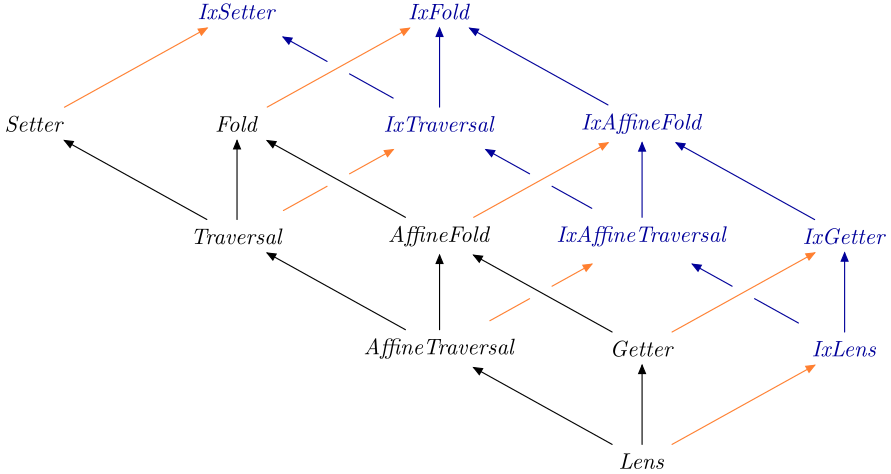
The details of how indexed optics work are beyond the scope of this blog post (see the indexed optics Haddocks if you are interested), but the diagram below shows that every optic above Lens in the subtype hierarchy has an accompanying indexed variant:

Summary

What are the key ideas underpinning the optics library?

• Every optic kind has a clear separation between interface and implementation, with a newtype abstraction boundary. This means the types reflect concepts such as lenses directly, rather than encoding them using higher-rank polymorphism. This leads to good type inference behaviour and (hopefully) clear error messages.

• The interface of each optic kind is clearly and systematically documented. See the documentation for Optics.Lens as an example.

• Since optics are not functions, they cannot be composed with the (.) operator. Instead a separate composition operator (%) is provided.

• Subtyping between different optic kinds (e.g. using a lens as a traversal) is accomplished using typeclasses. This is mostly automatic, although explicit casts are possible and occasionally necessary.

• Optics work with the OverloadedLabels GHC extension to allow the same name to be used for fields in different datatypes.

• Under the hood, optics uses the indexed profunctor encoding (rather than the van Laarhoven encoding used by lens). This allows us to support affine optics (which have at most one target). We provide conversions between the optics and lens representations; for isomorphisms and prisms these are in a separate package optics-vl as this incurs a dependency on profunctors.

• Indexed optics have a generally similar user experience to lens, but with different ergonomics (e.g. all optics are index-preserving, and there is no separate Conjoined class).

• The main Optics module exposes only a restricted selection of operators, making inevitably opinionated choices about which operators are the most generally useful.

• Sometimes functions in optics have a more specific type than the most general type possible, in the interests of simplicity and reducing the likelihood of errors. For example view does not work on folds, instead there is a separate function foldOf to eliminate folds, or gview if you really want additional polymorphism.

• For library writers who wish to define optics as part of their library interface, we provide a cut-down optics-core package with significant functionality but minimal dependencies (only GHC boot libraries). Unlike lens, it is not possible to define lenses without depending on at least optics-core.

For a full introduction to optics, check out the Haddocks for the main Optics module. We welcome feedback and contributions on the GitHub well-typed/optics repo.

Acknowledgements

I would like to thank my coauthors Andrzej Rybczak, Oleg Grenrus and Andres Löh for all their work on optics. Edsko de Vries, Alp Mestanogullari, Ömer Sinan Ağacan and other colleagues at Well-Typed gave helpful feedback on the library in general and this blog post in particular. Thanks are also due to Edward Kmett for his work on lens and for critiquing (though not necessarily endorsing!) the ideas behind this library.