An important factor affecting compilation speed and memory requirements is the
size of the core code generated by ghc from Haskell source modules. Thus, if
compilation time is an issue, this is something we should be conscious of and
optimize for. In part 1 of this blog post we took an in-depth look at
why certain Haskell constructs lead to quadratic blow-up in the generated ghc
core code, and how the large-records library avoids these
problems. Indeed, the large-records library provides support for records,
including support for generic programming, with a guarantee that the generated
core is never more than O(n) in the number of record fields.
The approach described there does however not directly apply to the case of
anonymous records. This is the topic we will tackle in this part 2.
Unfortunately, it seems that for anonymous records the best we can hope for is
O(n log n), and even to achieve that we need to explore some dark corners of
ghc. We have not attempted to write a new anynomous records library, but
instead consider the problems in isolation; on the other hand, the solutions we
propose should be applicable in other contexts as well. Apart from section
Putting it all together,
the rest of this blog post can be understood without having read part 1.
This work was done on behalf of Juspay; we will discuss the context in a bit more detail in the conclusions.
Recap: The problem of type arguments
Consider this definition of heterogenous lists, which might perhaps form the (oversimplified) basis for an anonymous records library:
data HList xs where
Nil :: HList '[]
(:*) :: x -> HList xs -> HList (x ': xs)If we plot the size of the core code generated by ghc for a Haskell module
containing only a single HList value
newtype T (i :: Nat) = MkT Word
type ExampleFields = '[T 00, T 01, .., , T 99]
exampleValue :: HList ExampleFields
exampleValue = MkT 00 :* MkT 01 :* .. :* MkT 99 :* Nilwe get an unpleasant surprise:
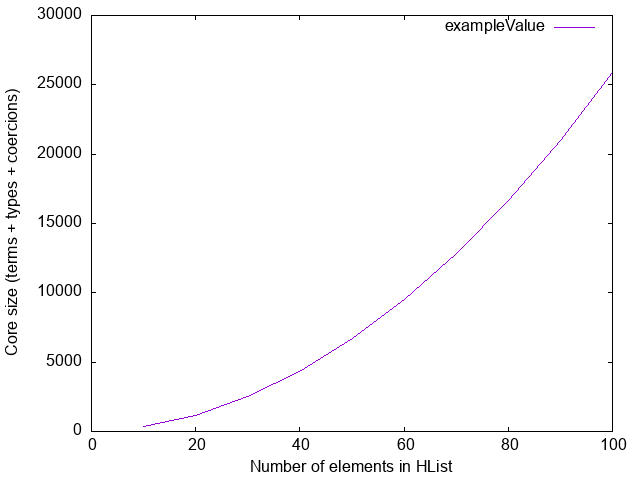
The source of this quadratic behaviour is type annotations. The translation of
exampleValue in ghc core is shown below (throughout this blog post I will
show “pseudo-core”, using standard Haskell syntax):
exampleValue :: HList ExampleFields
exampleValue =
(:*) @(T 00) @'[T 01, T 02, .., T 99] (MkT 00)
$ (:*) @(T 01) @'[ T 02, .., T 99] (MkT 01)
..
$ (:*) @(T 99) @'[ ] (MkT 99)
$ NilEvery application of the (:*) constructor records the names and types of the
remaining fields; clearly, this list is O(n) in the size of the record, and
since there are also O(n) applications of (:*), this term is O(n²) in the
number of elements in the HList.
We covered this in detail in part 1. In the remainder of this part 2 we
will not be concerned with values of HList (exampleValue), but only with
the type-level indices (ExampleFields).
Instance induction considered harmful
A perhaps surprising manifestation of the problem of quadratic type annotations arises for certain type class dictionaries. Consider this empty class, indexed by a type-level list, along with the customary two instances, for the empty list and an inductive instance for non-empty lists:
class EmptyClass (xs :: [Type])
instance EmptyClass '[]
instance EmptyClass xs => EmptyClass (x ': xs)
requireEmptyClass :: EmptyClass xs => Proxy xs -> ()
requireEmptyClass _ = ()Let’s plot the size of a module containing only a single usage of this function:
requiresInstance :: ()
requiresInstance = requireEmptyClass (Proxy @ExampleFields)Again, we plot the size of the module against the number of record fields
(number of entries in ExampleFields):
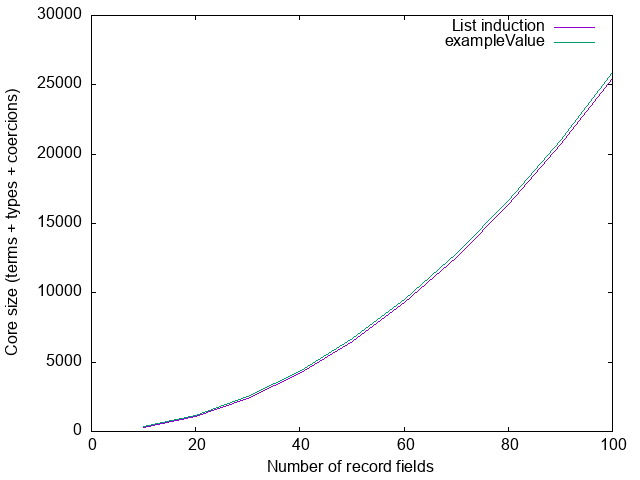
The size of this module is practically identical to the size of the module
containing exampleValue, because at the core level they actually look very
similar. The translation of requiresEmptyClass looks something like like this:
d00 :: EmptyClass '[T 00, T 01, .., T 99]
d01 :: EmptyClass '[ T 01, .., T 99]
..
d99 :: EmptyClass '[ T 99]
dNil :: EmptyClass '[ ]
d00 = fCons @'[T 01, T 02, .., T 09] @(T 00) d01
d01 = fCons @'[ T 02, .., T 99] @(T 01) d02
..
d99 = fCons @'[ ] @(T 99) dNil
dNil = fNil
requiresInstance :: ()
requiresInstance = requireEmptyClass @ExampleFields d00 (Proxy @ExampleFields)The two EmptyClass instances we defined above turn into two functions fCons
and fNil, with types
fNil :: EmptyClass '[]
fCons :: EmptyClass xs -> EmptyClass (x ': xs)which are used to construct dictionaries. These look very similar to the Nil
and (:*) constructor of HList, and indeed the problem is the same: we have
O(n) calls to fCons, and each of those records all the remaining fields,
which is itself O(n) in the number of record fields. Hence, we again have core
that is O(n²).
Note that this is true even though the class is empty! It therefore really does not matter what we put inside the class: any induction of this shape will immediately result in quadratic blow-up. This was already implicit in part 1 of this blog post, but it wasn’t as explicit as it perhaps should have been—at least, I personally did not have it as clearly in focus as I do now.
It is true that if both the module defining the instances and the module using the instance are compiled with optimisation enabled, that might all be optimised away eventually, but it’s not that easy to know precisely when we can depend on this. Moreover, if our goal is to improve compilation time (and therefore the development cycle), we anyway typically do not compile with optimizations enabled.
Towards a solution
For a specific concrete record we can avoid the problem by simply not using induction. Indeed, if we add
instance {-# OVERLAPPING #-} EmptyClass ExampleFieldsto our module, the size of the compiled module drops from 25,462 AST nodes to a
mere 15 (that’s 15 full stop, not 15k!). The large-records library takes
advantage of this: rather than using induction to define instances, it generates
a single instance for each record type, which has constraints for every field
in the record. The result is code that is O(n) in the size of the record.
The only reason large-records can do this, however, is that every record is
explicitly declared. When we are dealing with anonymous records such an
explicit declaration does not exist, and we have to use induction of some
form. An obvious idea suggests itself: why don’t we try halving the list at
every step, rather than reducing it by one, thereby reducing the code from
O(n²) to O(n log n)?
Let’s try. To make the halving explicit1, we define a binary
Tree type2, which we will use promoted to the type-level:
data Tree a =
Zero
| One a
| Two a a
| Branch a (Tree a) (Tree a)EmptyClass is now defined over trees instead of lists:
class EmptyClass (xs :: Tree Type) where
instance EmptyClass 'Zero
instance EmptyClass ('One x)
instance EmptyClass ('Two x1 x2)
instance (EmptyClass l, EmptyClass r) => EmptyClass ('Branch x l r)We could also change HList to be parameterized over a tree instead of a list
of fields. Ideally this tree representation should be an internal implementation
detail, however, and so we instead define a translation from lists to balanced
trees:
-- Evens [0, 1, .. 9] == [0, 2, 4, 6, 8]
type family Evens (xs :: [Type]) :: [Type] where
Evens '[] = '[]
Evens '[x] = '[x]
Evens (x ': _ ': xs) = x ': Evens xs
-- Odds [0, 1, .. 9] == [1, 3, 5, 7, 9]
type family Odds (xs :: [Type]) :: [Type] where
Odds '[] = '[]
Odds (_ ': xs) = Evens xs
type family ToTree (xs :: [Type]) :: Tree Type where
ToTree '[] = 'Zero
ToTree '[x] = 'One x
ToTree '[x1, x2] = 'Two x1 x2
ToTree (x ': xs) = 'Branch x (ToTree (Evens xs)) (ToTree (Odds xs))and then redefine requireEmptyClass to do the translation:
requireEmptyClass :: EmptyClass (ToTree xs) => Proxy xs -> ()
requireEmptyClass _ = ()The use sites (requiresInstance) do not change at all. Let’s measure again:
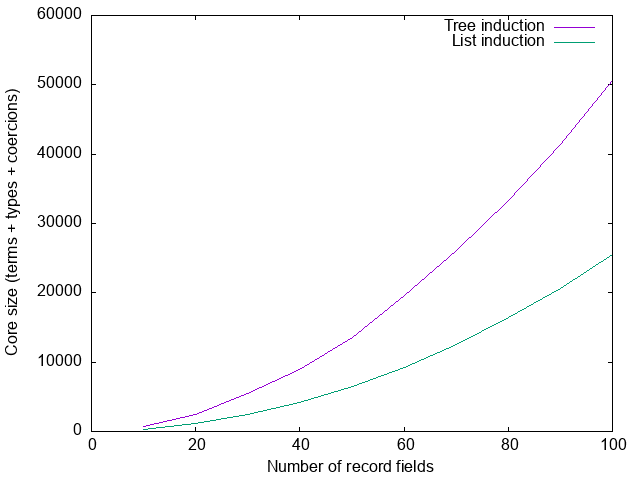
Total failure. Not only did we not improve the situation, it got significantly worse.
What went wrong?
To understand, let’s look at the case for when we have 10 record fields. The generated code looks about as clean as one might hope for:
dEx :: EmptyClass (ToTree ExampleFields)
dEx = dTree `cast` <..>
dTree :: EmptyClass (
'Branch
(T 0)
('Branch (T 1) ('Two (T 3) (T 7)) ('Two (T 5) (T 9)))
('Branch (T 2) ('Two (T 4) (T 8)) ('One (T 6)))
)
dTree =
fBranch
@('Branch (T 1) ('Two (T 3) (T 7)) ('Two (T 5) (T 9)))
@('Branch (T 2) ('Two (T 4) (T 8)) ('One (T 6)))
@(T 0)
( fBranch
@('Two (T 3) (T 7))
@('Two (T 5) (T 9))
@(T 1)
(fTwo @(T 3) @(T 7))
(fTwo @(T 5) @(T 9))
)
( -- .. right branch similar
)
requiresInstance :: ()
requiresInstance = requireEmptyClass @ExampleFields dEx (Proxy @ExampleFields)Each recursive call to the dictionary construction function fBranch is now
indeed happening at half the elements, as intended.
The need for a cast
The problem is in the first line:
dEx = dTree `cast` <..>Let’s first understand why we have a cast here at all:
The type of the function that we are calling is
requireEmptyClass :: forall xs. EmptyClass (ToTree xs) => Proxy xs -> ()We must pick a value for
xs: we pickExampleFields.In order to be able to call the function, we must produce evidence (that is, a dictionary) for
EmptyClass (ToTree ExampleFields). We therefore have to evaluateToTree ...to('Branch ...); as we do that, we construct a proofπthatToTree ...is indeed equal to the result(Branch ...)that we computed.We now have evidence of
EmptyClass ('Branch ...), but we need evidence ofEmptyClass (ToTree ...). This is where the cast comes in: we can coerce one to the other given a proof that they are equal; sinceπproves thatToTree ... ~ 'Branch ...we can construct a proof that
EmptyClass (ToTree ...) ~ EmptyClass ('Branch ...)by appealing to congruence (if
x ~ ythenT x ~ T y).
The part in square brackets <..> that I elided above is precisely this proof.
Proofs
Let’s take a closer look at what that proof looks like. I’ll show a simplified form3, which I hope will be a bit easier to read and in which the problem is easier to spot:
ToTree[3] (T 0) '[T 1, T 2, T 3, T 4, T 5, T 6, T 7, T 8, T 9]
; Branch (T 0)
( Evens[2] (T 1) (T 2) '[T 3, T 4, T 5, T 6, T 7, T 8, T 9]
; Evens[2] (T 3) (T 4) '[T 5, T 6, T 7, T 8, T 9]
; Evens[2] (T 5) (T 6) '[T 7, T 8, T 9]
; Evens[2] (T 7) (T 8) '[T 9]
; Evens[1] (T 9)
; ToTree[3] (T 1) '[T 3, T 5, T 7, T 9]
; Branch (T 1)
( Evens[2] (T 3) (T 5) '[T 7, T 9]
; Evens[2] (T 7) (T 9) '[]
; Evens[0]
; ToTree[2] (T 3) (T 7)
)
( Odds[1] (T 3) '[T 5, T 7, T 9]
; Evens[2] (T 5) (T 7) '[T 9]
; Evens[1] (T 9)
; ToTree[2] (T 5) (T 9)
)
)
( Odds[1] (T 1) '[T 2, T 3, T 4, T 5, T 6, T 7, T 8, T 9]
; .. -- omitted (similar to the left branch)
)The “axioms” in this proof – ToTree[3], Evens[2], etc. – refer to specific
cases of our type family definitions. Essentially the proof is giving us a
detailed trace of the evaluation of the type families. For example, the proof
starts with
ToTree[3] (T 0) '[T 1, T 2, T 3, T 4, T 5, T 6, T 7, T 8, T 9]which refers to the fourth line of the ToTree definition
ToTree (x ': xs) = 'Branch x (ToTree (Evens xs)) (ToTree (Odds xs))recording the fact that
ToTree '[T 0, .., T 9]
~ 'Branch (T 0) (ToTree (Evens '[T 1, .. T9])) (ToTree (Odds '[T 1, .. T9]))The proof then splits into two, giving a proof for the left subtree and a proof for the right subtree, and here’s where we see the start of the problem. The next fact that the proof establishes is that
Evens '[T 1, .. T 9] ~ '[T 1, T 3, T 5, T 7, T 9]Unfortunately, the proof to establish this contains a line for every evaluation step:
Evens[2] (T 1) (T 2) '[T 3, T 4, T 5, T 6, T 7, T 8, T 9]
; Evens[2] (T 3) (T 4) '[T 5, T 6, T 7, T 8, T 9]
; Evens[2] (T 5) (T 6) '[T 7, T 8, T 9]
; Evens[2] (T 7) (T 8) '[T 9]
; Evens[1] (T 9)We have O(n) such steps, and each step itself has O(n) size since it records
the remaining list. The coercion therefore has size O(n²) at every branch in
the tree, leading to an overall coercion also4 of size O(n²).
Six or half a dozen
So far we defined
requireEmptyClass :: EmptyClass (ToTree xs) => Proxy xs -> ()
requireEmptyClass _ = ()and are measuring the size of the core generated for a module containing
requiresInstance :: ()
requiresInstance = requireEmptyClass (Proxy @ExampleFields)for some list ExampleFields. Suppose we do one tiny refactoring, and make
the caller use ToList instead; that is, requireEmptyClass becomes
requireEmptyClass :: EmptyClass t => Proxy t -> ()
requireEmptyClass _ = ()and we now call ToTree at the use site instead:
requiresInstance :: ()
requiresInstance = requireEmptyClass (Proxy @(ToTree ExampleFields))Let’s measure again:
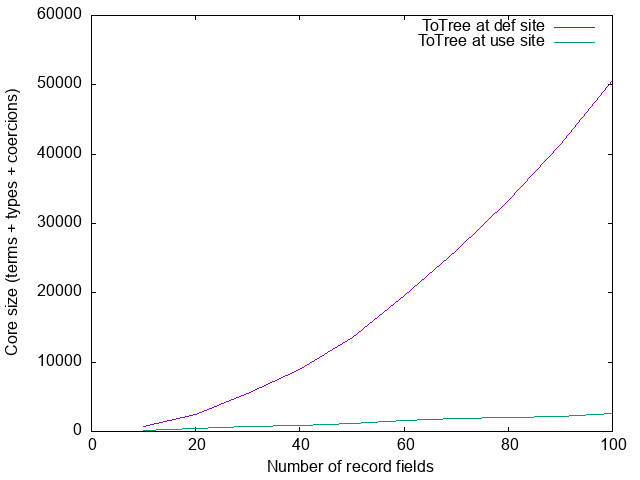
The quadratic blow-up disappeared! What happened? Just to add to the confusion,
let’s consider one other small refactoring, leaving the definition of
requireEmptyClass the same but changing the use site to
requiresInstance = requireEmptyClass @(ToTree ExampleFields) ProxyMeasuring one more time:
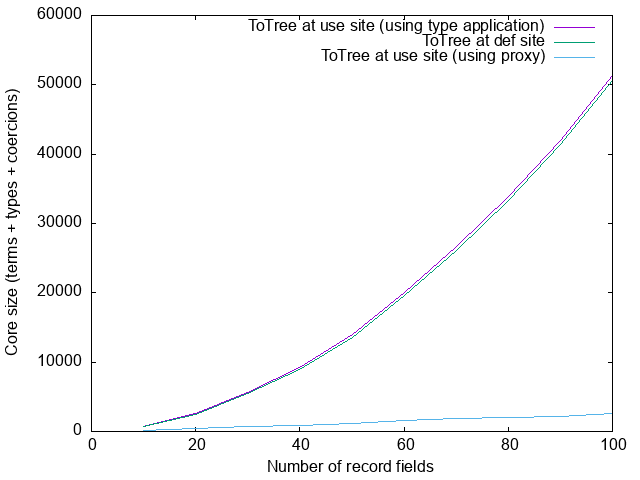
Back to blow-up! What’s going on?
Roles
We will see in the next section that the difference is due to roles. Before we look at the details, however, let’s first remind ourselves what roles are5. When we define
newtype Age = MkAge Intthen Age and Int are representationally equal but not nominally equal:
if we have a function that wants an Int but we pass it an Age, the type
checker will complain. Representational equality is mostly a run-time concern
(when do two values have the same representation on the runtime heap?), whereas
nominal equality is mostly a compile-time concern. Nominal equality implies
representional equality, of course, but not vice versa.
Nominal equality is a very strict equality. In the absence of type families, types are only nominally equal to themselves; only type families introduce additional axioms. For example, if we define
type family F (a :: Type) :: Type where
F Int = Bool
F Age = Charthen F Int and Bool are considered to be nominally equal.
When we check whether two types T a and T b are nominally equal, we must
simply check that a and b are nominally equal. To check whether T a and
T b are representionally equal is however more subtle [Safe zero-cost
coercions for Haskell, Fig 3]. There are three cases to consider,
illustrated by the following examples:
data T1 x = T1
data T2 x = T2 x
data T3 x = T3 (F x)Then
T1 aandT1 bare representionally equal no matter the values ofaandb: we say thatxhas a phantom role.T2 aandT2 bare representionally equal ifaandbare:xhas a representional role.T3 aandT3 bare representionally equal ifaandbare nominally equal:xhas a nominal role (T3 IntandT3 Ageare certainly not representionally equal, even thoughIntandAgeare!).
This propagates up; for example, in
data ShowType a = ShowType {
showType :: Proxy a -> String
}the role of a is phantom, because a has a phantom role in Proxy. The roles
of type arguments are automatically inferred, and usually the only interaction
programmers have with roles is through
coerce :: Coercible a b => a -> bwhere Coercible is a thin layer around representational equality.
Roles thus remain invisible most of the time—but not today.
Proxy versus type argument
Back to the problem at hand. To understand what is going on, we have to be very precise. The function we are calling is
requireEmptyClass :: EmptyClass xs => Proxy xs -> ()
requireEmptyClass _ = ()The question we must carefully consider is: what are we instantiating xs to?
In the version with the quadratic blowup, where the use-site is
requiresInstance = requireEmptyClass @(ToTree ExampleFields) Proxywe are being very explicit about the choice of xs: we are instantiating it to
ToTree ExampleFields. In fact, we are more explicit than we might realize: we
are instantiating it to the unevaluated type ToTree ExampleFields, not to
('Branch ...). Same thing, you might object, and you’d be right—but also
wrong. Since we are instantiating it to the unevaluated type, but then build a
dictionary for the evaluated type, we must then cast that dictionary; this is
precisely the picture we painted in section What went wrong?
above.
The more surprising case then is when the use-site is
requiresInstance = requireEmptyClass (Proxy @(ToTree ExampleFields))In this case, we’re leaving ghc to figure out what to instantiate xs to.
It will therefore instantiate it with some fresh variable 𝜏. When it then
discovers that we also have a Proxy 𝜏 argument, it must unify 𝜏 with
ToTree ExampleFields. Crucially, when it does so, it instantiates 𝜏 to
the evaluated form of ToTree ExampleFields (i.e., Branch ...), not the
unevaluated form. In other words, we’re effectively calling
requiresInstance = requireEmptyClass @(Branch _ _ _) (Proxy @(ToTree ExampleFields))Therefore, we need and build evidence for EmptyClass (Branch ...), and there
is no need for a cast on the dictionary.
However, the need for a cast has not disappered: if we instantiate xs to
(Branch ...), but provide a proxy for (ToTree ...), we need to cast the
proxy instead—so why the reduction in core size? Let’s take a look at the
equality proof given to the cast:
Univ(phantom phantom <Tree *>
-- (1) (2) (3) (4)
:: ToTree ExampleFields -- (5)
, 'Branch (T 0) -- (6)
('Branch (T 1)
('Two (T 3) (T 7))
('Two (T 5) (T 9)))
('Branch (T 2)
('Two (T 4) (T 8))
('One (T 6)))
)This is it! The entire coercion that was causing us trouble has been replaced basically by a single-constructor “trust me” universal coercion. This is the only coercion that establishes “phantom equality”6. Let’s take a closer look at the coercion:
Univindicates that this is a universal coercion.- The first occurrence of
phantomis the role of the equality that we’re establishing. - The second occurrence of
phantomis the provenance of the coercion: what justifies the use of a universal coercion? Here this isphantomagain (we can use a universal coercion when establishing phantom equality), but this is not always the case; one example isunsafeCoerce, which can be used to construct a universal coercion between any two types at all7. - When we establish the equality of two types 𝜏1 :: 𝜅1 and 𝜏2 :: 𝜅2, we
also need to establish that the two kinds 𝜅1 and 𝜅2 are equal. In our
example, both types trivially have the same kind, and so we can just use
<Tree *>: reflexivity for kindTree *.
Finally, (5) and (6) are the two types that we are proving to be equal to each other.
This then explains the big difference between these two definitions:
requiresInstance = requireEmptyClass (Proxy @(ToTree ExampleFields))
requiresInstance = requireEmptyClass @(ToTree ExampleFields) ProxyIn the former, we are instantiating xs to (Branch ...) and we need to
cast the proxy, which is basically free due to Proxy’s phantom type argument;
in the latter, we are instantiating xs to (ToTree ...), and we need to
cast the dictionary, which requires the full equality proof.
Incoherence
If a solution that relies on the precise nature of unification, instantiating type variables to evaluated types rather than unevaluated types, makes you a bit uneasy—I would agree. Moreover, even if we did accept that as unpleasant but necessary, we still haven’t really solved the problem. The issue is that
requireEmptyClass :: EmptyClass xs => Proxy xs -> ()
requireEmptyClass _ = ()is a function we cannot abstract over: the moment we define something like
abstracted :: forall xs. EmptyClass (ToTree xs) => Proxy xs -> ()
abstracted _ = requireEmptyClass (Proxy @(ToTree xs))in an attempt to make that ToTree call a responsibility of a library instead
of use sites (after all, we wanted the tree representation to be an
implementation detail), we are back to the original problem.
Let’s think a little harder about these roles. We finished the previous section
with a remark that “(..) we need to cast the dictionary, which requires the
full equality proof”. But why is that? When we discussed roles above,
we saw that the a type parameter in
data ShowType a = ShowType {
showType :: Proxy a -> String
}has a phantom role; yet, when we define a type class
class ShowType a where
showType :: Proxy a -> String(which, after all, is much the same thing), a is assigned a nominal role,
not a phantom role. The reason for this is that ghc insists on coherence (see
Safe zero-cost coercions for Haskell, section 3.2, Preserving class coherence).
Coherence simply means that there is only ever a single instance of a class
for a specific type; it’s part of how ghc
prevents ambiguity during instance resolution.
We can override the role of the ShowType dictionary and declare it to be
phantom
type role ShowType phantombut we lose coherence:
data ShowTypeDict a where
ShowTypeDict :: ShowType a => ShowTypeDict a
showWithDict :: Proxy a -> ShowTypeDict a -> String
showWithDict p ShowTypeDict = showType p
instance ShowType Int where showType _ = "Int"
showTypeInt :: ShowTypeDict Int
showTypeInt = ShowTypeDict
oops :: String
oops = showWithDict (Proxy @Bool) (coerce showTypeInt)This means that the role annotation for ShowType requires the
IncoherentInstances language pragma (there is currently
no class-level pragma).
Solving the problem
Despite the problem with roles and potential incoherence discussed in the
previous section, role annotations on classes cannot make instance resolution
ambiguous or result in runtime type errors or segfaults. We do have to be
cautious with the use of coerce, but we can shield the user from this through
careful module exports. Indeed, we have used role annotations on type classes
to our advantage before.
Specifically, we can redefine our EmptyClass as an internal (not-exported)
class as follows:
class EmptyClass' (xs :: Tree Type) -- instances as before
type role EmptyClass' phantomthen define a wrapper class that does the translation from lists to trees:
class EmptyClass' (ToTree xs) => EmptyClass (xs :: [Type])
instance EmptyClass' (ToTree xs) => EmptyClass (xs :: [Type])
requireEmptyClass :: EmptyClass xs => Proxy xs -> ()
requireEmptyClass _ = ()Now the translation to a tree has become an implementation detail that users do not need to be aware of, whilst still avoiding (super)quadratic blow-up in core:
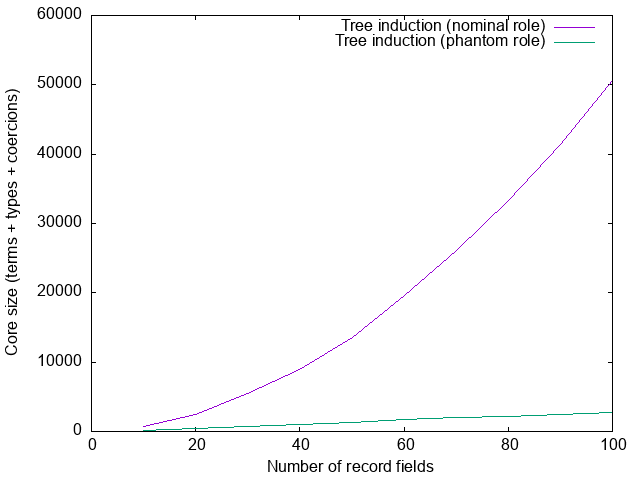
Constraint families
There is one final piece to the puzzle. Suppose we define a type family mapping types to constraints:
type family CF (a :: Type) :: ConstraintIn the next session we will see a non-contrived example of this; for now, let’s
just introduce a function that depends on CF a for no particular reason at all:
withCF :: CF a => Proxy a -> ()
withCF _ = ()Finally, we provide an instance for HList:
type instance CF (HList xs) = EmptyClass (ToTree xs)Now let’s measure the size of the core generated for a module containing a single call
satisfyCF :: ()
satisfyCF = withCF (Proxy @(HList ExampleFields))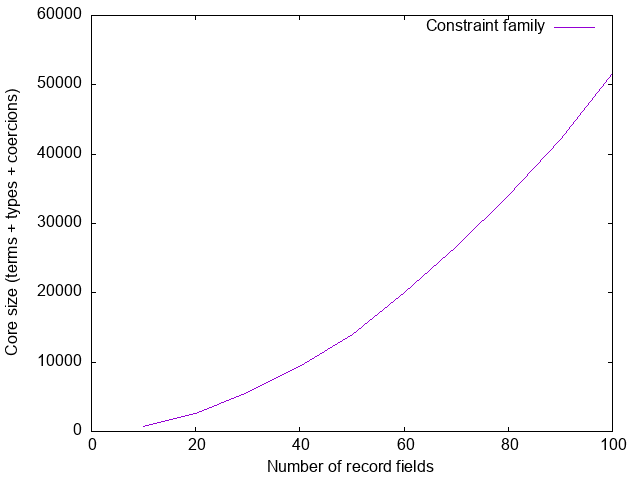
Sigh.
Shallow thinking
In section Proxy versus type argument above, we saw that when we call
requireEmptyClass @(Branch _ _ _) (Proxy @(ToTree ExampleFields))we construct a proof π :: Proxy (ToTree ...) ~ Proxy (Branch ...), which
then gets simplified. We didn’t spell out in detail how that simplification
happens though, so let’s do that now.
As mentioned above, the type checker always works with nominal equality. This
means that the proof constructed by the type checker is actually π :: Proxy (ToTree ...) ~N Proxy (Branch ...). Whenever we cast something in core,
however, we want a proof of representational equality. The coercion language
has an explicit constructor for this8, so we could construct the
proof
sub π :: Proxy (ToTree ...) ~R Proxy (Branch ...)However, the function that constructs this proof first takes a look: if it is
a constructing an equality proof T π' (i.e., an appeal to congruence for type
T, applied to some proof π'), where T has an argument with a phantom role,
it replaces the proof (π') with a universal coercion instead. This also
happens when we construct a proof that EmptyClass (ToTree ...) ~R EmptyClass (Branch ...) (like in section Solving the problem),
provided that the argument to EmptyClass is declared to have a phantom role.
Why doesn’t that happen here? When we call function withCF we need to
construct evidence for CF (HList ExampleFields). Just like before, this means
we must first evaluate this to EmptyClass (Branch ..), resulting in a proof of
nominal equality π :: CF .. ~N EmptyClass (Branch ..). We then need to change
this into a proof of representational equality to use as an argument to cast.
However, where before π looked like Proxy π' or EmptyClass π', we now have
a proof that looks like
D:R:CFHList[0] <'[T 0, T 1, .., T 9]>_N
; EmptyClass π'which first proves that CF (HList ..) ~ EmptyClass (ToTree ..), and only
then proves that EmptyClass (ToTree ..) ~ EmptyClass (Branch ..). The
function that attempts the proof simplification only looks at the top-level of
the proof, and therefore does not notice an opportunity for simplification here
and simply defaults to using sub π.
The function does not traverse the entire proof because doing so at every point
during compilation could be prohibitively expensive. Instead, it does cheap
checks only, leaving the rest to be cleaned up by coercion optimization.
Coercion optimization is part of the “very simple optimizer”, which runs even
with -O0 (unless explicitly disabled with -fno-opt-coercion). In this
particular example, coercion optimization will replace the proof (π') by a
universal coercion, but it will only do so later in the compilation pipeline;
better to reduce the size of the core sooner rather than later. It’s also not
entirely clear if it will always be able to do so, especially also because the
coercion optimiser can make things significantly worse in
some cases, and so it may be scaled back in the future. I think it’s preferable
not to depend on it.
Avoiding deep normalization
As we saw, when we call
withCF (Proxy @(HList ExampleFields))the type checker evaluates CF (HList ExampleFields) all the way to EmptyClass (Branch ...): although there is ghc ticket proposing to change
this, at present whenever ghc evaluates a type, it
evaluates it all the way. For our use case this is frustrating: if ghc
were to rewrite CF (HList ..) to ExampleFields (ToTree ..) (with a tiny
proof: just one rule application), we would then be back where we were in
section Solving the problem, and we’d avoid the
quadratic blow-up. Can we make ghc stop evaluating earlier? Yes, sort of. If
instead of
type instance CF (HList xs) = EmptyClass (ToTree xs)we say
class EmptyClass (ToTree xs) => CF_HList xs
instance EmptyClass (ToTree xs) => CF_HList xs
type instance CF (HList xs) = CF_HList xsthen CF (HList xs) simply gets rewritten (in one step) to CF_HList xs, which
contains no further type family applications. Now the type checker needs to
check that CF_HList ExampleFields is satisfied, which will match the above
instance, and hence it must check that EmptyClass (ToTree ExampleFields) is
satisfied. Now, however, we really are back in the situation from
section Solving the problem, and the size of our core
looks good again:
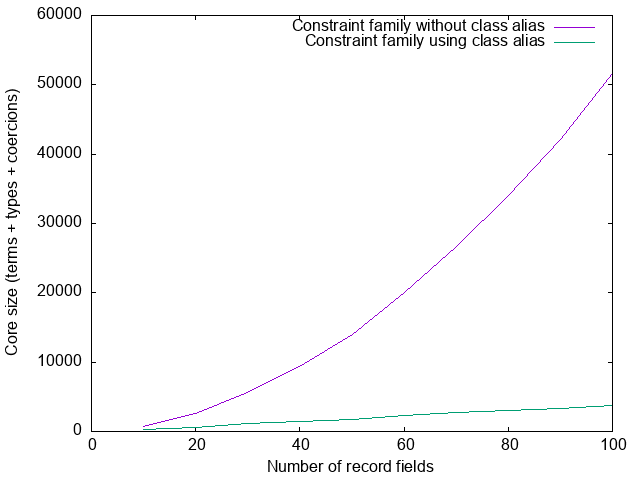
Putting it all together: Generic instance for HList
Let’s put theory into practice and give a Generic instance for HList,
of course avoiding quadratic blow-up in the process. We will use the Generic
class from the large-records library, discussed at length in part 1.
The first problem we have to solve is that when giving a Generic instance
for some type a, we need to choose a constraint
Constraints a c :: (Type -> Constraint) -> Constraintsuch that when Constraints a c is satisfied, we can get a type class
dictionary for c for every field in the record:
class Generic a where
-- | @Constraints a c@ means "all fields of @a@ satisfy @c@"
type Constraints a (c :: Type -> Constraint) :: Constraint
-- | Construct vector of dictionaries, one for each field of the record
dict :: Constraints a c => Proxy c -> Rep (Dict c) a
-- .. other class members ..Recall that Rep (Dict c) a is a vector containing a Dict c x for every field
of type x in the record. Since we are avoiding heterogenous data structures
(due to the large type annotations), we effectively need to write a function
hlistDict :: Constraints a c => Proxy a -> [Dict c Any]Let’s tackle this in quite a general way, so that we can reuse what we develop
here for the next problem as well. We have a type-level list of types of the
elements of the HList, which we can translate to a type-level tree of types.
We then need to reflect this type-level tree to a term-level tree with values
of some type f Any (in this example, f ~ Dict c). We will delegate
reflection of the values in the tree to a separate class:
class ReflectOne (f :: Type -> Type) (x :: Type) where
reflectOne :: Proxy x -> f Any
class ReflectTree (f :: Type -> Type) (xs :: Tree Type) where
reflectTree :: Proxy xs -> Tree (f Any)
type role ReflectTree nominal phantom -- critical!Finally, we can then flatten that tree into a list, in such a way that it
reconstructs the order of the list (i.e., it’s a term-level inverse to the
ToTree type family):
treeToList :: Tree a -> [a]The instances for ReflectTree are easy. For example, here is the instance
for One:
instance ReflectOne f x => ReflectTree f ('One x) where
reflectTree _ = One (reflectOne (Proxy @x))The other instances for ReflectTree follow the same structure (the full source
code can be found in the large-records test suite). It
remains only to define a ReflectOne instance for our current specific use
case:
instance c a => ReflectOne (Dict c) (a :: Type) where
reflectOne _ = unsafeCoerce (Dict :: Dict c a)With this definition, a constraint ReflectTree (Dict c) (ToTree xs) for a
specific list of xs will result in a c x constraint for every x in xs,
as expected. We are now ready to give a partial implementation of the Generic
class:
hlistDict :: forall c (xs :: [Type]).
ReflectTree (Dict c) (ToTree xs)
=> Proxy xs -> [Dict c Any]
hlistDict _ = treeToList $ reflectTree (Proxy @(ToTree xs))
class ReflectTree (Dict c) (ToTree xs) => Constraints_HList xs c
instance ReflectTree (Dict c) (ToTree xs) => Constraints_HList xs c
instance Generic (HList xs) where
type Constraints (HList xs) = Constraints_HList xs
dict _ = Rep.unsafeFromListAny $ hlistDict (Proxy @xs)The other problem that we need to solve is that we need to construct field metadata for every field in the record. Our (over)simplified “anonymous record” representation does not have field names, so we need to make them up from the type names. Assuming some type family
type family ShowType (a :: Type) :: Symbolwe can construct this metadata in much the same way that we constructed the dictionaries:
instance KnownSymbol (ShowType a) => ReflectOne FieldMetadata (a :: Type) where
reflectOne _ = FieldMetadata (Proxy @(ShowType a)) FieldLazy
instance ReflectTree FieldMetadata (ToTree xs) => Generic (HList xs) where
metadata _ = Metadata {
recordName = "Record"
, recordConstructor = "MkRecord"
, recordSize = length fields
, recordFieldMetadata = Rep.unsafeFromListAny fields
}
where
fields :: [FieldMetadata Any]
fields = treeToList $ reflectTree (Proxy @(ToTree xs))The graph below compares the size of the generated core between a
straight-forward integration with generics-sop and two
integrations with large-records, one in which the ReflectTree
parameter has its inferred nominal role, and one with the phantom role
override:
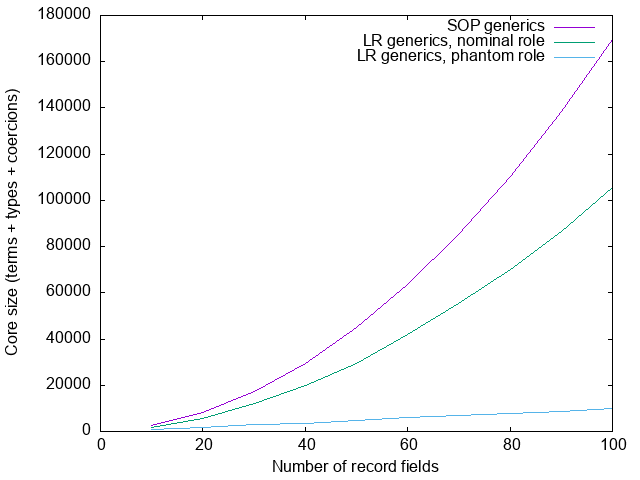
Both the generics-sop integration and the nominal large-records integration
are O(n²). The constant factors are worse for generics-sop, however,
because it suffers from both the problems described in part 1 of this
blog as well as the problems described in this part 2. The nominal
large-records integration only suffers from the problems described in part 2,
which are avoided by the O(n log n) phantom integration.
TL;DR: Advice
We considered a lot of deeply technical detail in this blog post, but I think it can be condensed into two simple rules. To reduce the size of the generated core code:
- Use instance induction only with balanced data structures.
- Use expensive type families only in phantom contexts.
where “phantom context” is short-hand for “as an argument to a datatype, where that argument has a phantom role”. The table below summarizes the examples we considered in this blog post.
| Don’t | Do |
|---|---|
instance C xs => instance C (x ': xs)
|
instance (C l, C r) => instance C ('Branch l r)
|
foo @(F xs) Proxy
|
foo (Proxy @(F xs))
|
type role Cls nominal
|
type role Cls phantomUse with caution: requires IncoherentInstances
|
type instance F a = Expensive a
|
type instance F a = ClassAlias a(for F a :: Constraint)
|
Conclusions
This work was done in the context of trying to improve the compilation time of
Juspay’s code base. When we first started analysing why
Juspay was suffering from such long compilation times, we realized that a large
part of the problem was due to the large core size generated by ghc when using
large records, quadratic in the number of record fields. We therefore developed
the large-records library, which offers support for records
which guarantees to result in core code that is linear in the size of the
record. A first integration attempt showed that this improved compilation time
by roughly 30%, although this can probably be tweaked a little further.
As explained in MonadFix’s blog post Transpiling a
large PureScript codebase into Haskell, part 2: Records are
trouble, however, some of the records
in the code base are anonymous records, and for these the large-records
library is not (directly) applicable, and instead, MonadFix is using their own
library jrec.
An analysis of the integration with large-records revealed however that these
large anonymous records are causing similar problems as the named records did.
Amongst the 13 most expensive modules (in terms of compilation time), 5 modules
suffered from huge coercions, with less extreme examples elsewhere in the
codebase. In one particularly bad example, one function contained coercion
terms totalling nearly 2,000,000 AST nodes! (The other problem that stood out
was due to large enumerations, not something I’ve thought much about yet.)
We have certainly not resolved all sources of quadratic core code for anonymous
records in this blog post, nor have we attempted to integrate these ideas in
jrec. However, the generic instance for anonymous records (using
generics-sop generics) was particularly troublesome, and the ideas outlined
above should at least solve that problem.
In general the problem of avoiding generating superlinear core is difficult and multifaceted:
- We need a way in
ghccore to access and update record and type class dictionary fields without mentioning all fields in those records. - We need a solution for all the type arguments. Perhaps one option is to improve control sharing at the type level; a long-standing problem. Perhaps we need more dramatic changes such as Scrap your type applications. Research from the world of dependently typed languages such as A dependently typed calculus with pattern matching and erasure inference may also provide insights.
- We need to improve the representation of coercions. The 2013 paper Evidence normalization in System FC introduced the concept of coercion optimization, but it is woefully inadequate in the presence of type family reduction. There is some ongoing work on improving the situation, as well as some proposals for specific stop-gap measures (e.g., see MR #6680) but there is still a long way to go.
Fortunately, ghc gives us just enough leeway that if we are very careful
we can avoid the problem. That’s not a solution, obviously, but at least there
are temporary work-arounds we can use.
Postscript: Pre-evaluating type families
If the evaluation of type families at compile time leads to large proofs,
one for every step in the evaluation, perhaps we can improve matters by
pre-evaluating these type families. For example, we could define ToTree
as
type family ToTree (xs :: [Type]) :: Tree Type where
ToTree '[] = 'Zero
ToTree '[x0] = 'One x0
ToTree '[x0, x1] = 'Two x0 x1
ToTree '[x0, x1, x2] = 'Branch x0 ('One x1) ('One x2)
ToTree '[x0, x1, x2, x3] = 'Branch x0 ('Two x1 x3) ('One x2)
ToTree '[x0, x1, x2, x3, x4] = 'Branch x0 ('Two x1 x3) ('Two x2 x4)
ToTree '[x0, x1, x2, x3, x4, x5] = 'Branch x0 ('Branch x1 ('One x3) ('One x5)) ('Two x2 x4)
...perhaps (or perhaps not) with a final case that defaults to regular evaluation.
Now ToTree xs can evaluate in a single step for any of the pre-computed cases.
Somewhat ironically, in this case we’re better off without phantom contexts:
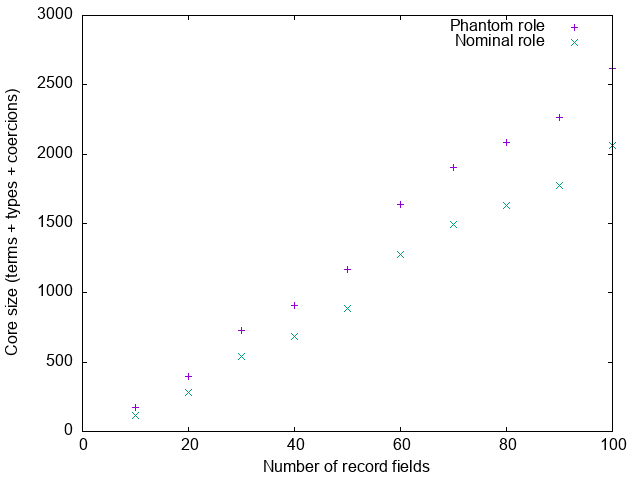
The universal coercion is now larger than the regular proof, because it records the full right-hand-side of the type family:
Univ(phantom phantom <Tree *>
:: 'Branch
(T 0)
('Branch (T 1) ('Two (T 3) (T 7)) ('Two (T 5) (T 9)))
('Branch (T 2) ('Two (T 4) (T 8)) ('One (T 6)))
, ToTree '[T 0, T 1, T 2, T 3, T 4, T 5, T 6, T 7, T 8, T 9]))The regular proof instead only records the rule that we’re applying:
D:R:ToTree[10] <T 0> <T 1> <T 2> <T 3> <T 4> <T 5> <T 6> <T 7> <T 8> <T 9>Hence, the universal coercion is O(n log n), whereas the regular proof is
O(n). Incidentally, this is also the reason why ghc doesn’t just always
use universal coercions; in some cases the universal coercion can be
significantly larger than the regular proof (the Rep type family of
GHC.Generics being a typical example). The difference between O(n)
and O(n log n) is of course significantly less important than the difference
between O(n log n) and O(n²), especially since we anyway still have other
O(n log n) factors, so if we can precompute type families like this, perhaps
we can be less careful about roles.
However, this is only a viable option for certain type families. A full-blown
anonymous records library will probably need to do quite a bit of type-level
computation on the indices of the record. For example, the classical
extensible records theory by Gaster and Jones depends crucially
on a predicate lacks that checks that a particular field is not already
present in a record. We might define this as
type family Lacks (x :: k) (xs :: [k]) :: Bool where
Lacks x '[] = 'True
Lacks x (x ': xs) = 'False
Lacks x (y ': xs) = Lacks x xsIt’s not clear to me how to pre-compute this type family in such a way that the
right-hand side can evaluate in O(1) steps, without the type family needing
O(n²) cases. We might attempt
type family Lacks (x :: k) (xs :: [k]) :: Bool where
-- 0
Lacks x '[] = 'True
-- 1
Lacks x '[x] = 'False
Lacks x '[y] = 'True
-- 2
Lacks x '[x , y2] = 'False
Lacks x '[y1 , x ] = 'False
Lacks x '[y1 , y2] = 'True
-- 3
Lacks x '[x, y2 , y3] = 'False
Lacks x '[y1, x , y3] = 'False
Lacks x '[y1, y2 , x ] = 'False
Lacks x '[y1, y2 , y3] = 'True
-- etcbut even if we only supported records with up to 200 fields, this would require over 20,000 cases. It’s tempting to try something like
type family Lacks (x :: k) (xs :: [k]) :: Bool where
Lacks x [] = True
Lacks x [y0] = (x != y0)
Lacks x [y0, y1] = (x != y0) && (x != y1)
Lacks x [y0, y1, y2] = (x != y0) && (x != y1) && (x != y2)
..but that is not a solution (even supposing we had such an != operator): the
right hand side still has O(n) operations, and so this would still result in
proofs of O(n) size, just like the non pre-evaluated Lacks definition. Type
families such as Sort would be more difficult still. Thus, although
precomputation can in certain cases help avoid large proofs, and it’s a useful
technique to have in the arsenal, I don’t think it’s a general solution.
Footnotes
The introduction of the
Treedatatype is not strictly necessary. We could instead work exclusively with lists, and useEvens/Oddsdirectly to split the list in two at each step. The introduction ofTreehowever makes this structure more obvious, and as a bonus leads to smaller core, although the difference is a constant factor only.↩︎This
Treedata type is somewhat non-standard: we have values both at the leaves and in the branches, and we have leaves with zero, one or two values. Having values in both branches and leaves reduces the number of tree nodes by one half (leading to smaller core), which is an important enough improvement to warrant the minor additional complexity. TheTwoconstructor only reduces the size the tree roughly by a further 4%, so not really worth it in general, but it’s useful for the sake of this blog post, as it keeps examples of trees a bit more manageable.↩︎Specifically, I made the following simplifications to the actual coercion proof:
1. Drop the use ofSym, replacingSym (a ; .. ; c)by(Sym c ; .. ; Sym a)andSym cby simplycfor atomic axiomsc.
2. Appeal to transitivity to replacea ; (b ; c)bya ; b ; c
3. Drop all explicit use of congruence, replacingT cby simplyc, wheneverThas a single argument.
4. As a final step, reverse the order of the proof; in this case at least,ghcseemed to reason backwards from the result of the type family application, but it’s more intuitive to reason forwards instead.↩︎See Master Theorem, case 3: Work to split/recombine a problem dominates subproblems.↩︎
Roles were first described in Generative Type Abstraction and Type-level Computation. Phantom roles were introduced in Safe zero-cost coercions for Haskell.↩︎
Safe zero-cost coercions for Haskell does not talk about this in great detail, but does mention it. See Fig 5, “Formation rules for coercions”, rule
Co_Phantom, as well as the (extremely brief) section 4.2.2., “Phantom equality relates all types”. The paper does not use the terminology “universal coercion”.↩︎Confusingly the pretty-printer uses a special syntax for a universal unsafe coercion, using
UnsafeCoinstead ofUniv.↩︎Safe zero-cost coercions for Haskell, section 4.2.1: Nominal equality implies representational equality.↩︎
